|
Nonlinear Dynamics and Complexity in
Optical Physics:
Nonlinear
Optoelectronic Image Processing
Parallel image processing and particularly detection and tracking of
moving objects underpins many military and commercial applications. At present existing image technology is
neither fast enough nor sufficiently flexible to handle real-time and
high-resolution data of low contrast and in cluttered scenes. This programme undertakes research on
novel nonlinear partial-differential equation based algorithms for
real-time and high-resolution signal processing, and from this to develop a
hybrid nonlinear opto-electronic device to undertake these tasks. The novelty of this project is three
fold: development of nonlinear PDE algorithms for real-time and
high-resolution image processing, experimental implementation of such
algorithms using a hybrid optical-electronic architecture, and use of
electronically programmable nonlinearity with diffractive optical feedback
and system integration with adaptive optics in the hybrid system. Latest developments in optical
micro-electro-mechanical systems and microelectronics make possible the
full integration of the hybrid system to a compact device. The subject of this research is currently
a mainline research activity worldwide.
This programme involves QinetiQ in the UK
and the Army Research Lab (ARL) in the USA.
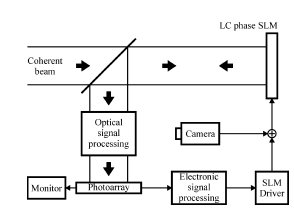
The proposed image-processing system is a generic hybrid opto-electronic
device, comprising a phase spatial light modulator (SLM) coupled with a
photo-detector array through a combined optical and electronic feedback
loop. As shown in the schematic,
images under investigation are introduced to the system via the SLM as phase
modulations on a coherent laser beam when it reflects from the SLM. Before they are fed back to the SLM, the
phase modulations are processed, both optically and electronically
according to which is best suited for a particular task. For example, (optical) wave diffraction
for image edge enhancement and (electronic) Kerr nonlinearity for phase
distortion compensation. From a
theoretical point of view, the experiment can be accurately modelled by a
set of coupled partial differential equations (PDE). Our simulation results, examples of which
are shown below, will therefore provide a reliable guideline to the
experiment.
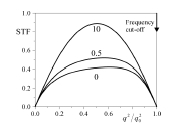
Figure: Spatiotemporal Transfer
Function for objects of three different velocities. q/q0 is the normalised transverse wave
number.

Figure: (a) input image shows a
moving object from t = 0 to t = 300; (b) a snapshot of output image after
suppression of background; (c) and (d) the original and processed image of
a snapshot of a video stream showing a moving car in country road.
Back to Research Reviews'
Page
|