|
Copyright (C) 1999
Nonlinear
Dynamics Group at Heriot-Watt University and Computational Biology Group at University of Leeds

Nonlinear Analysis of
Ventricular Fibrillation

Nonlinear
Analysis of Simulated ECGs of Ventricular Fibrillation
--The temporal evolution of ventricular
fibrillation revealed with Poincare sections
Michael
Smalla, Dejin Yua, Robert G. Harrisona,
Richard Claytonb and Arun Holdenb
aNonlinear Dynamics Group at Heriot-Watt University
bComputational Biology Group at University of Leeds
We
apply a new version of the Poincare section technique to simulated and
clinically recorded ECG data during ventricular fibrillation and observe
similar structural features in both groups. For computational simulations
of ventricular fibrillation in ``heart-like'' tissue, we are able to
successively reconstruct equivalent dynamics from each of three independent
scalar time series, for each of three distinct simulations. Hence we
conclude that ECG pad placement is not critical for this technique. As we
observe similar dynamical time dependence in both simulated and clinical
data we conclude that the simulation (Fitz-Hugh Nagumo dynamics in a cuboid
caricature of the myocardium) exhibits dynamic features qualitatively
similar to real ventricular fibrillation. Quantitative
similarity has previously been observed.
1.
Poincare Sections
A reconstruction of dynamics is required from the observed time
series data prior to nonlinear analysis. Let xt (t = 1, 2, 3,
..., N) be a scalar time series (one of the pseudo-ECG observables, or the
scalar ECG measured by a defibrillator), one chooses a ``suitable'' values
of T (delay time) and de (embedding dimension) and reconstructs
the underlying dynamics according to the map (Taken's embedding theorem)
Xt
= (xt, xt-T, xt-2T,..., xt-(de-1)T)
Thus a vector series Xt (t = 1, 2, 3, ..., N-(de-1)T)
is reconstructed.
A simple Poincare section can be obtained in the following way. Let
H be a hyper-surface in a de-dimensional space Rde
(H is (de-1)-dimensional), such that H intersects Xt,
and all intersections of Xt and H are orthogonal. Let s1,
s2, ... ... be the times that Xt intersects H in a
particular direction (every second intersection). Then the Poincare section
is a plot of Xsi vs. Xsi+1 and the first return map
is the nonlinear function relating Xsi to Xsi+1.
Figure 1 illustrates the construction of a first return map from
intersection of a trajectory Xt and a hyper-surface H.
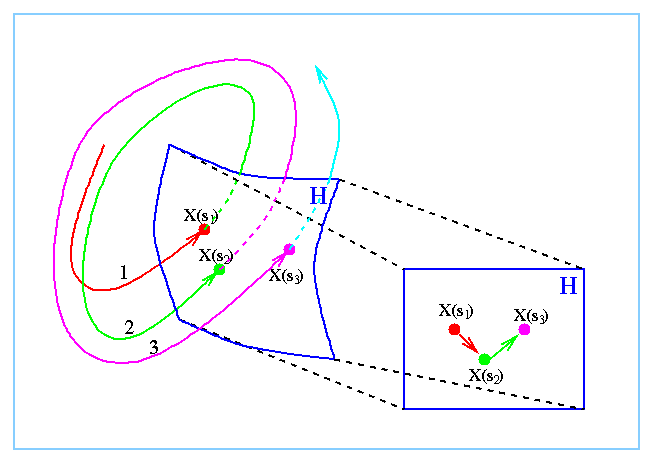
Figure 1: A schematic representation of the computation of a first
return map, and temporal colour-coded Poincare section. The trajectory x(t)
(in black) intersects the surface H (in blue, on the left) at x(s1),
x(s2), and x(s3). We examine the relative position, ordering
and structure of the points x(si) on a projection of H (on the
right).
The method of Poincare sections is usually applied to experimental
time series by examining interspike intervals (e.g. RR intervals) or
successive amplitudes (i.e. peak-trough values). However, these techniques
are somewhat limited. In the following, we introduce a new version of
Poincare section, apply this new technique to analyse simulated ECG signals
and compare with clinical recordings of VF. To this end, we select a vector
W from Rde, and project Zt onto W.
Let
Wt
= ProjWZt = W.Zt/||W||
and calculate s1, s2, ... ... as the time when
Wt has a local maximum. The Poincare time series is then Xsi
(i = 1, 2, ..., k). Potentially one may define the Poincare series to be
multiple components of Zsi (i = 1, 2, ..., k), but with a
careful choice of W the first component is often sufficient.
2.
Simulated and Clinical VF ECG data
We use two sets of data in this study. The first are computational
simulations of electrical wave propagation and the second set of data are
recorded from defibrillators on board ambulances.
1) Simulated
ECG data
We used a cuboid of 100 x 100 x 50 units with Fitz-Hugh Nagumo
excitability (diffusion coefficient 1, beta = 0.75, gamma = 0.50, and
epsilon = 0.30 ) to produce a numerical caricature of re-entrant waves in
the myocardium. We solved the three dimensional cable equations for the
excitation variable u and the recovery variable v (time step of 0.03 time
units, space step of 0.50 space units). A typical snapshot of the
excitation variable u is shown in figure 2 (left panel).
In each case we computed the pseudo-ECG Ex,y,z
along each of the coordinate axes as a weighted average of the gradient of
u:
Ex =
SUM [u(i-1,0,0) - u(i,0,0)]/i
Ey =
SUM [u(0,j-1,0) - u(0,j,0)]/j
Ez =
SUM [u(0,0,k-1) - u(0,0,k)]/k
where sums are taken over i = 2, ..., 100, j = 2, ..., 100 and k =
2, ..., 50. Each simulation consists of a vector time series Ex,
Ey and Ez of 5000 points sampled at
0.03 time units. Three
simulated ECGs are shown in figure 2 (right panel).
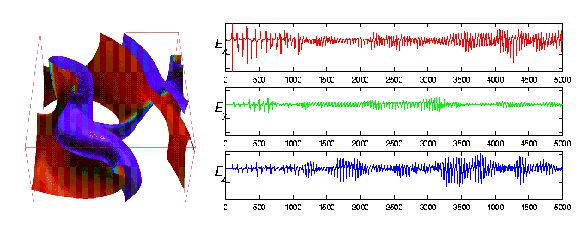
Figure 2: (Left) A snapshot of the excitation variable u during one
of computational simulations of multiple reentry waves in cuboid of
``heart-like'' tissue. (Right) Three components of one simulation. The Ex,
Ey, and Ez component are shown here.
This simulation was initiated with a single, bent, spiral wave. The
vertical axis is datum number, the horizontal axis is arbitrary but equal
in each case. Note that each of the three components appear, visually,
quite distinct.
2) Clinical ECG data
Episodes of ventricular fibrillation and response to defibrillation
shocks were recorded by a Laerdal defibrillator on board ambulances in the
Norwegian ambulance service. Data was recorded at a frequency of 100 Hz and
a resolution of 8 bits. In the previous study, each data set was then
classified according to the dominant rhythm; (1) Pulse (sinus rhythm), (2)
No pulse, (3) Isoelectric (Asystole), (4) Non-continuous ventricular
fibrillation, and (5) Continuous ventricular fibrillation. The length of
recording (typically 20 - 60 seconds) in each case varies, but in general
it corresponds to the period from the end of cardio-pulmonary resuscitation
until the next defibrillation shock. The period proceeding the first shock
or subsequent to the last may also be recorded. In some recordings
interference from CPR is noticeable at the start of the recording (these
time series have been excluded from this study).
From 836 recordings of 108 subjects we selected 47 recordings from
14 subjects on the basis of length of recording, digital resolution and
lack of noise and artifacts for further analysis. Results for these 47 data
sets are described in this study.
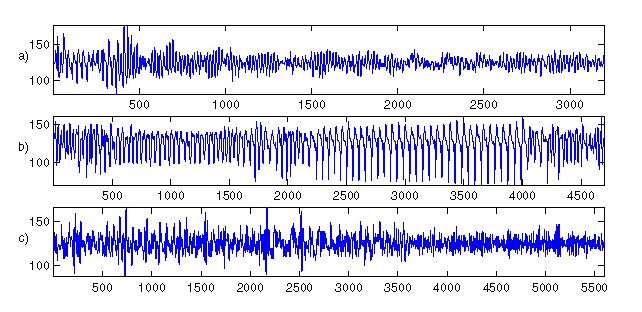
Figure 3: Three clinical recordings from a Laerdal defibrillator on
board a Norwegian ambulance. Three patients are: a) h104cmbw1s1, b)
h383cmbw2s2, and c) h282cmbw5s4. Note that panel a) and c) exhibit no
obvious time dependent features in there dynamics, panel b) does.
3.
Results
1) Simulated VF
Each of the three simulated ``pseudo-ECG'' time series we generated
mimics the break down of spiral waves during the initiation of VF. Figure 2
shows one of the simulated recordings. Figure 4 shows the Poincare sections
estimated from the data of figure 2. The qualitative features in each
reconstruction are identical -- the orientation and proportion is different
for each reconstruction, but the shape is essentially the same. That is,
these three reconstructions share the same topology. The dynamics in each
case are clearly equivalent.
Furthermore the dynamics revealed here are clearly time dependent.
The initial first return map is basically ``L'' shaped, this corresponds to
a stage when substantial organisation is still present in the simulation
(coloured in blues). The first return map dynamics then change to the
regions coloured in light blues through to light oranges. Finally, a third
distinct region is evident in the part of the first return map coloured
red. These same three distinct regions may be observed in each of these
three reconstructions from three linearly independent time series (Ex,
Ey, and Ez).
Note that different choice of projection vector W will yield substantially
different results. We have selected one of the dominant eigenvectors as
this yields good results for this data. However, different choice of vector
will produce different, equally correct, results. We are simply selecting
the two dimensional view that shows, most clearly, the features we wish to
emphasise.
These calculations have also been conducted for the other two
simulations described above. Similar results were obtained for this data.
In each case the three components (Ex, Ey,
and Ez) produced equivalent results. Furthermore, the
same broad features were observed in each simulation. The results we have presented in
figure 4 are representative.
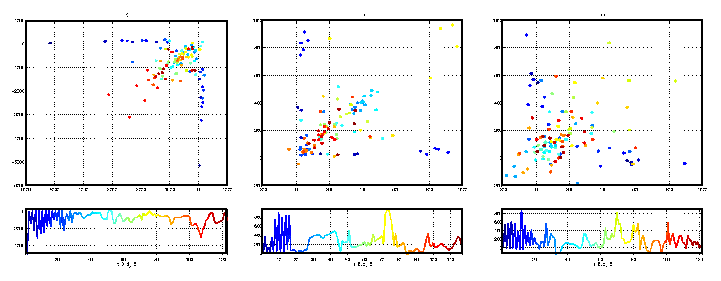
Figure 4: Estimated Poincare sections for the data illustrated in
figure 2. From left to right, we have illustrated the reconstructed
Poincare sections for Ex, Ey, and Ez.
The Poincare intersections are ordered and coloured according to that ordering.
The ordering is the same from figure to figure, but as the reconstruction
in each case is different the exact number of Poincare intersections (and
therefore the exact colouration) is not the same. In each set of panels,
the top panel is the 2 dimensional embedding (first return map) of
successive scalar Poincare sections, shown (as a time series) in the lower
panel. The choice of embedding parameters (de and T) is given
below each panel.
2) Actual VF timeseries
In this section we present the results of the estimation of some
first return maps for clinically recorded data (section 2.2). The main
point we wish to emphasise here is that some of these data sets exhibit
features that are qualitatively similar to the results in section 3.1
(figure 4). We do not claim to observe the same features in all the
clinical data set, nor do we claim to provide a clinically significant
discriminant. We only wish to demonstrate that the computational
simulations, and real ventricular fibrillation share some common,
non-trivial, features.
Figure 5 shows three dynamical reconstruction from the clinical
recordings in three different subjects, depicted in Figure 3. Two of these
data sets exhibit obvious similarities to the results obtained for the
computational simulations, the third (figure 5, panel c) exhibits more
subtle time dependent dynamics in the first returns map. Panels a) and b)
exhibit not only the characteristic ``L'' shape of the first return maps,
as in figure 4, but also three separate phases in the dynamics. In panel a)
of figure 5, these are coloured dark blue, light blue to green, and orange
to red, respectively. In panel b) the dark blue and red phases seem to
coincide, marking a return to the initial dynamics late in the time series.
The intermediate phase however is distinct (coloured light blue) and
similar to the second and third phases in the computational simulations. In
figure 5, panel c) has less obvious time dependent structure, the dark blue
points are arranged in a vague ``L'' shape. The light blue to green, and
orange to read points are approximately diagonal (and perpendicular to one
another).
We applied these techniques to 47 recordings from 14 subjects, each
with a variety of embedding parameters (de, T, and W). Of these,
28 recordings from 13 subjects exhibited some time dependent dynamics in
the first return map. Some of these dynamics changes were fairly obvious
and may have been observed directly from the time series, some of them were
fairly subtle. Many of the time series were particularly short making
discrimination a difficult and possibly subjective task. However, the
results presented in figure 5 are typical. Figure 5 panel a) is a definite
positive results, panel b) is perhaps more borderline, and panel c) is
perhaps the most subtle of the positive results.
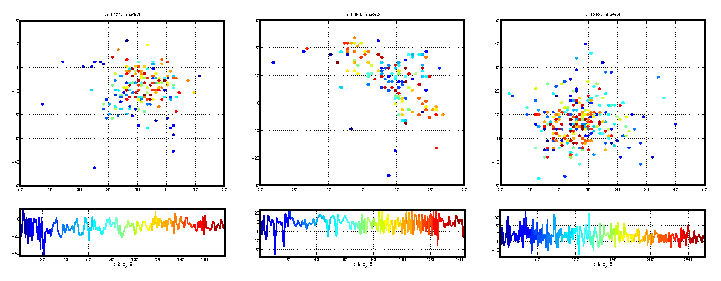
Figure 5: Estimated Poincare sections for the three time series
illustrated in figure 3. Panels a), b), and c) of this figure correspond,
respectively, to panels a), b), and c) of figure 3. The Poincare
intersections are ordered and coloured according to that ordering. The
ordering is the same from figure to figure, but as the time series are
recordings of separate events, the exact number of Poincare intersections
(and therefore the exact colouration) is not the same. In each set of
panels, the top panel is the 2 dimensional embedding (first return map) of
successive scalar Poincare sections, shown (as a time series) in the lower
panel. The choice of embedding parameters (de and T) is given
below each panel. Panel a) and b) exhibit obvious similarities to the
Poincare sections represented in figure 4. Panel c) exhibits no obvious
time dependence and stands in stark contrast to the other results.
4.
Concluding remarks
Our calculations with computational simulations of the
electrocardiogram during ventricular fibrillation demonstrate the method of
first return maps, as described in this paper, may be applied to clinical data
and produce results that are independent of the exact placement of ECG pads
on the torso. Furthermore, we observed three distinct phases in the
temporal evolution of the computational simulations. These phase correspond
to three stages in the spiral wave break up; from a single meandering
spiral to multiple wavelets.
Furthermore, we observed in clinical data sets recorded in humans
during naturally occurring ventricular fibrillation, topological features
similar to those observed in the simulations. Hence we are able to conclude
that the dynamics of the simulated ECG are qualitatively similar to those
observed in reality.
As this technique detects the degree of organisation of spiral waves
in the myocardium, this may offer a useful technique to estimate the degree
of organisation or degeneracy from a single lead ECG in a clinical setting.
Moreover, this technique offers a method which is not only independent of
the placement of the ECG pad, but is also robust for short and noisy time
series.
Back to Research Reviews' Page
|